Dimensi Besaran
19.52
Diposting oleh Melany Christy
Catatan :
Semua besaran fisis dalam mekanika dapat dinyatakan dengan tiga besaran pokok (Dimensi Primer) yaitu panjang, massa dan waktu. Sebagaimana terdapat Satuan Besaran Turunan yang diturunkan dari Satuan Besaran Pokok, demikian juga terdapat Dimensi Primer dan Dimensi Sekunder yang diturunkan dari Dimensi Primer.
Berikut adalah tabel yang menunjukkan dimensi dan satuan tujuh besaran dasar dalam sistem SI.

Manfaat Dimensi dalam Fisika antara lain : (1) dapat digunakan untuk membuktikan dua besaran sama atau tidak. Dua besaran sama jika keduanya memiliki dimensi yang sama atau keduanya termasuk besaran vektor atau skalar, (2) dapat digunakan untuk menentukan persamaan yang pasti salah atau mungkin benar, (3) dapat digunakan untuk menurunkan persamaan suatu besaran fisis jika kesebandingan besaran fisis tersebut dengan besaran-besaran fisis lainnya diketahui.
Satuan dan dimensi suatu variabel fisika adalah dua hal berbeda. Satuan besaran fisis didefinisikan dengan perjanjian, berhubungan dengan standar tertentu (contohnya, besaran panjang dapat memiliki satuan meter, kaki, inci, mil, atau mikrometer), namun dimensi besaran panjang hanya satu, yaitu L. Dua satuan yang berbeda dapat dikonversikan satu sama lain (contohnya: 1 m = 39,37 in; angka 39,37 ini disebut sebagai faktor konversi), sementara tidak ada faktor konversi antarlambang dimensi.
ANALISIS DIMENSI
Analisis dimensi adalah cara yang sering dipakai dalam fisika, kimia dan teknik untuk memahami keadaan fisis yang melibatkan besaran yang berbeda-beda. Analisis dimensi selalu digunakan untuk memeriksa ketepatan penurunan persamaan. Misalnya, jika suatu besaran fisis memiliki satuan massa dibagi satuan volume namun persamaan hasil penurunan hanya memuat satuan massa, persamaan tersebut tidak tepat. Hanya besaran-besaran berdimensi sama yang dapat saling ditambahkan, dikurangkan atau disamakan. Jika besaran-besaran berbeda dimensi terdapat di dalam persamaan dan satu sama lain dibatasi tanda “+” atau “-” atau “=”, persamaan tersebut harus dikoreksi terlebih dahulu sebelum digunakan. Jika besaran-besaran berdimensi sama maupun berbeda dikalikan atau dibagi, dimensi besaran-besaran tersebut juga terkalikan atau terbagi. Jika besaran berdimensi dipangkatkan, dimensi besaran tersebut juga dipangkatkan.
Seringkali kita dapat menentukan bahwa suatu rumus salah hanya dengan melihat dimensi atau satuan dari kedua ruas persamaan. Sebagai contoh, ketika kita menggunakan rumus A= 2.Phi.r untuk menghitung luas. Dengan melihat dimensi kedua ruas persamaan, yaitu [A] = L2 dan [2.phi.r] = L kita dengan cepat dapat menyatakan bahwa rumus tersebut salah karena dimensi kedua ruasnya tidak sama. Tetapi perlu diingat, jika kedua ruas memiliki dimensi yang sama, itu tidak berarti bahwa rumus tersebut benar. Hal ini disebabkan pada rumus tersebut mungkin terdapat suatu angka atau konstanta yang tidak memiliki dimensi, misalnya Ek = 1/2 mv2 , di mana 1/2 tidak bisa diperoleh dari analisis dimensi.
Anda harus ingat karena dalam suatu persamaan mungkin muncul angka tanpa dimensi, maka angka tersebut diwakili dengan suatu konstanta tanpa dimensi, misalnya konstanta k.
Contoh Soal : menentukan dimensi suatu besaran
Tentukan dimensi dari besaran-besaran berikut ini : (a) volum, (b) massa jenis, (c) percepatan, (d) usaha
Petunjuk : anda harus menulis rumus dari besaran turunan yang akan ditentukan dimensinya terlebih dahulu. Selanjutnya rumus tersebut diuraikan sampai hanya terdiri dari besaran pokok.
Jawaban :
(a) Persamaan Volum adalah hasil kali panjang, lebar dan tinggi di mana ketiganya memiliki dimensi panjang, yakni [L]. Dengan demikian, Dimensi Volum :
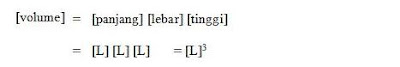
(b) Persamaan Massa Jenis adalah hasil bagi massa dan volum. Massa memiliki dimensi [M] dan volum memiliki dimensi [L]3. Dengan demikian Dimensi massa jenis :

(c) Persamaan Percepatan adalah hasil bagi Kecepatan (besaran turunan) dengan Waktu, di mana Kecepatan adalah hasil bagi Perpindahan dengan Waktu. Oleh karena itu, kita terlebih dahulu menentukan dimensi Kecepatan, kemudian dimensi Percepatan.

(d) Persamaan Usaha adalah hasil kali Gaya (besaran Turunan) dan Perpindahan (dimensi = [L]), sedang Gaya adalah hasil kali massa (dimensi = [M]) dengan percepatan (besaran turunan). Karena itu kita tentukan dahulu dimensi Percepatan (lihat (c)), kemudian dimensi Gaya dan terakhir dimensi Usaha.

Konversi Satuan
14.31
Diposting oleh Melany Christy
Besaran apapun yang kita ukur, seperti panjang, massa atau kecepatan, terdiri dari angka dan satuan. Sering kita diberikan besaran dalam satuan tertentu dan kita kita ingin menyatakannya dalam satuan lain. Misalnya kita mengetahui jarak dua kota dalam satuan kilometer dan kita ingin mengetahui berapa jaraknya dalam satuan meter. Demikian pula dengan massa benda. Misalnya kita mengukur berat badan kita dalam satuan kg dan kita ingin mengetahui berat badan kita dalam satuan ons atau pon. Untuk itu kita harus mengkonversi satuan tersebut. Konversi berarti mengubah. Untuk mengkonversi satuan, terlebih dahulu harus diketahui beberapa hal yang penting, antara lain awalan-awalan metrik yang digunakan dalam satuan dan faktor konversi.
Awalan-awalan satuan yang sering digunakan dapat anda lihat pada tabel berikut ini.
Kelebihan sistem Satuan Internasional (SI) adalah kemudahan dalam pemakaiannya karena menggunakan sistem desimal (kelipatan 10) dan hanya ada satu satuan pokok untuk setiap besaran dengan penambahan awalan untuk satuan yang lebih besar atau lebih kecil. Misalnya, 1 centimeter = 0,01 meter atau 1 kilogram sama dengan 1000 gram. Untuk kemudahan mengubah suatu satuan ke satuan lain dapat dilakukan dengan menggunakan bantuan tangga konversi seperti yang terlihat pada gambar di bawah ini.
Cara mengkonversi satuan-satuan SI dengan tangga konversi :
Pertama, Letakkan satuan asal yang akan dikonversi dan satuan baru yang akan dicari pada tangga sesuai dengan urutan tangga konversi
Kedua, Hitung jumlah langka yang harus ditempuh dari satuan asal ke satuan baru
a. Jika satuan baru berada di bawah satuan asal ( menuruni tangga ), maka :
- Setiap turun satu tangga, bilangan asal dikali 10
- Setiap turun dua tangga, bilangan asal dikali 10
- Setiap turun tiga tangga, bilangan asal dikali 1000, dan seterusnya
b. Jika satuan baru berada di atas satuan asal ( menaiki tangga ), maka :
- Setiap naik satu tangga, bilangan asal dibagi 10
- Setiap naik dua tangga, bilangan asal dibagi 100
- Setiap naik tiga tangga, bilangan asal dibagi 1000, dan seterusnya
Contoh soal :
Ubahlah satuan berikut ini :
10 km = …. cm ?
Perhatikan Tangga Konversi Satuan Panjang.
Dari km (kilometer) ke cm (centimeter), kita menuruni 5 anak tangga. Dengan demikian kita mengalikannya dengan 100.000 (5 nol). Jadi 10 km = 10 x 100000 = 1000.000 cm
7000 m = ….. km ?
Perhatikan Tangga Konversi Satuan Panjang.
Dari m (meter) ke km (kilometer), kita menaiki 3 anak tangga. Dengan demikian kita membaginya dengan 1000 (3 nol). Jadi 7000 km = 7000 : 1000 = 7 km
300 gr = ….. kg ?
Perhatikan Tangga Konversi Satuan massa.
Dari gr (gram) ke kg (kilogram), kita menaiki 3 anak tangga. Dengan demikian kita membaginya dengan 1000 (3 nol). Jadi 300 gr = 300 : 1000 = 0,3 kg
5 kg = …. mg ?
Perhatikan Tangga Konversi Satuan massa.
Dari kg (kilogram) ke mg (miligram), kita menuruni 6 anak tangga. Dengan demikian kita mengalikannya dengan 1.000.000 (6 nol). Jadi 5 kg = 5 x 1000.000 = 5.000.000 kg
FAKTOR KONVERSI
Selain mengkonversi satuan dalam sistem internasional, kita juga harus mengetahui konversi satuan dalam sistem yang berbeda, antara lain dari satuan Sistem Internasional ke Sistem British atau sebaliknya. Sebagai contoh, kita mengukur panjang sebuah meja dalam satuan inchi dan kita ingin menyatakannya dalam centimeter. Untuk itu kita perlu mengetahui faktor konversi. Faktor konversi dapat anda lihat pada tabel di bawah ini.
Contoh Soal :
Ubahlah satuan panjang berikut ini :
15 inchi = ….. m ?
Perhatikan Faktor Konversi Panjang.
1 inchi = 2,54 cm. —– 1 cm = 0,01 m (lihat tangga konversi panjang)
Jadi, 15 inchi = 15 x 2,54 cm = 38,1 cm —— 38,1 cm = 38,1 x 0,01 m = 0,381 meter.
100 mil = …. cm ?
Perhatikan Faktor Konversi Panjang.
1 mil = 1,61 km. —– 1 km = 100.000 cm (lihat tangga konversi panjang)
Jadi, 100 mil = 100 x 1,61 km = 161 km —- 161 km = 161 x 100.000 cm
= 16.100.000 cm.
100 km = …. mil ?
Perhatikan Faktor Konversi Panjang.
1 km = 0,621 mil.
Jadi, 100 km = 100 x 0,621 mil = 62,1 mil.
Ubahlah satuan Kelajuan berikut ini :
(Catatan : Knot merupakan satuan kelajuan yang biasa digunakan Kapal Laut)
50 Knot = …. km/jam ?
Perhatikan Faktor Konversi Panjang.
1 knot = 1,151 mil/jam —– 1 mil/jam = …. Km/jam ?
1 mil = 1,61 km (lihat Faktor Konversi Panjang)
Jadi, 1 mil/jam = 1,61 km/jam
1,151 mil/jam = 1,85311 km/jam
50 Knot = 50 (1,151 mil/jam) = 50 (1,85311 km/jam) = 92,6555 km/jam
Satuan Besaran Fisis
14.28
Diposting oleh Melany Christy
Untuk mencapai suatu tujuan tertentu di dalam fisika, kita biasanya melakukan pengamatan yang disertai dengan pengukuran. Pengamatan suatu gejala secara umum tidak lengkap apabila tidak disertai data kuantitatif yang didapat dari hasil pengukuran. Lord Kelvin, seorang ahli fisika berkata, bila kita dapat mengukur yang sedang kita bicarakan dan menyatakannya dengan angka-angka, berarti kita mengetahui apa yang sedang kita bicarakan itu.
Apa yang Anda lakukan sewaktu melakukan pengukuran? Misalnya anda mengukur panjang meja belajar dengan menggunakan jengkal, dan mendapatkan bahwa panjang meja adalah 6 jengkal. Jadi, mengukur adalah membandingkan sesuatu yang diukur dengan sesuatu lain yang sejenis yang ditetapkan sebagai satuan. Dalam pengukuran di atas Anda telah mengambil jengkal sebagai satuan panjang.
Sebelum adanya standar internasional, hampir tiap negara menetapkan sistem satuannya sendiri. Penggunaan bermacam-macam satuan untuk suatu besaran ini menimbulkan kesukaran. Kesukaran pertama adalah diperlukannya bermacam-macam alat ukur yang sesuai dengan satuan yang digunakan. Kesukaran kedua adalah kerumitan konversi dari satu satuan ke satuan lainnya, misalnya dari jengkal ke kaki. Ini disebabkan tidak adanya keteraturan yang mengatur konversi satuan-satuan tersebut.
Akibat kesukaran yang ditimbulkan oleh penggunaan sistem satuan yang berbeda maka muncul gagasan untuk menggunakan hanya satu jenis satuan saja untuk besaran-besaran dalam ilmu pengetahuan alam dan teknologi. Suatu perjanjian internasional telah menetapkan satuan sistem internasional (Internasional System of Units) disingkat satuan SI. Satuan SI ini diambil dari sistem metrik yang telah digunakan di Perancis. Selain Sistem Internasional (SI), terdapat juga Sistem Satuan Britania (British System) yang juga sering digunakan dalam kehidupan sehari-hari.
SISTEM INTERNASIONAL (SI)
Satuan pengukuran dalam Sistem Internasional (SI), dibedakan atas statis dan dinamis. Sistem dinamis terdiri dari dua jenis yaitu sistem satuan dinamis besar dan dinamis kecil. Sistem dinamis besar biasa disebut “MKS” atau “sistem praktis” atau “sistem Giorgie”, sedangkan sistem dinamis kecil biasa kita sebut “CGS” atau “sistem Gauss”.
Satuan Besaran Pokok (Sistem Internasional/SI)
Karena hanya ada tujuh besaran pokok maka hanya terdapat tujuh satuan pokok yang dapat anda dilihat pada tabel di bawah ini :
| Besaran Pokok | Lambang | Satuan MKS dan Singkatan | Satuan CGS dan Singkatan |
| Panjang | l (length) | Meter (m) | Centimeter (cm) |
| massa | m (mass) | Kilogram (Kg) | Gram (gr) |
| Waktu | t (time) | Detik / Sekon (s) | Sekon (s) |
| Suhu | T (Temperature) | Kelvin (K) | |
| Kuat Arus | I | Ampere (A) | |
| Jumlah Molekul | Mole (Mol) | ||
| Intensitas Cahaya | Candela (Cd) |
Penetapan Satuan / Definisi Satuan
Penetapan satuan SI dilakukan oleh CGPM, yaitu suatu badan yang bernaung di bawah organisasi Internasional Timbangan dan Ukuran (OIPM-Organisation Internationale des Poids et Measures ). Tugas badan ini adalah mengadakan konferensi sedikitnya satu kali dalam enam tahun dan mengesahkan ketentuan baru dalam bidang metrologi dasar.
1. Meter
Definisi lama : Satu meter adalah 1.650.763,73 kali panjang gelombang cahaya merah jingga yang dipancarkan isotop krypton 86.
Definisi baru (yang digunakan saat ini) : satu meter adalah jarak yang ditempuh cahaya (dalam vakum) dalam selang waktu 1/299 792 458 sekon
2. Kilogram
Satu kilogram (Kg) adalah massa sebuah kilogram standar (silinder platina iridium) yang aslinya disimpan di lembaga Timbangan dan Ukuran Internasional (CGPM ke-1, 1899) di Serves, Perancis. (gambar kilogram standar)
3. Sekon / Detik
Satu sekon (s) adalah selang waktu yang diperlukan oleh atom sesium-133 untuk melakukan getaran sebanyak 9 192 631 770 kali dalam transisi antara dua tingkat energi di tingkat energi dasarnya (CGPM ke-13; 1967)
4. Kelvin
Satu Kelvin (K) adalah 1/273,16 kali suhu termodinamika titik tripel air (CGPM ke-13, 1967). Dengan demikian, suhu termodinamika titik tripel air adalah 273,16 K. Titik tripel air adalah suhu dimana air murni berada dalam keadaan seimbang dengan es dan uap jenuhnya.
5. Ampere
Satu Ampere (A) adalah kuat arus tetap yang jika dialirkan melalui dua buah kawat yang sejajar dan sangat panjang, dengan tebal yang dapat diabaikan dan diletakkan pada jarak pisah 1 meter dalam vakum, menghasilkan gaya 2 X 10-7 newton pada setiap meter kawat.
6. Candela
Satu Candela (Cd) adalah intensitas cahaya suatu sumber cahaya yang memancarkan radiasi monokromatik pada frekuensi 540 X 1012 hertz dengan intensitas radiasi sebesar 1/683 watt per steradian dalam arah tersebut (CGPM ke-16, 1979)
7. Mol
Satu mol zat terdiri atas 6,025 x 1023 buah partikel. ( 6,025 x 1023 disebut dengan bilangan avogadro ).
Satuan Besaran Turunan (Sistem Internasional/SI)
Contoh satuan-satuan besaran turunan dapat anda lihat pada tabel di bawah ini. Penjelasan mengenai bagaimana memperoleh satuan Besaran Turunan akan dipelajari pada pembahasan tentang Dimensi Besaran.
| Besaran Turunan | Lambang | Satuan dan Singkatan |
| Luas | L | Meter kuadrat (m2) |
| Volume | V (volume) | Meter kubik (m3) |
| Kecepatan | v (velocity) | “Meter per sekon” (m/s) |
| Percepatan | A (acceleration) | Meter “per sekon kuadrat” (m/s2) |
| Massa Jenis | (rho) | Kg/m3 |
| Gaya | w (weight) | Kg m/s2 = Newton (N) |
| Usaha dan energi | W ( | Kg m2/s2 = joule (J) |
| Daya | P (power) | Kg m2/s3 = watt (W) |
| Tekanan | P (pressure) | Kg/m s2 = Pascal (Pa) |
SATUAN SISTEM BRITANIA ( BRITISH SYSTEM )
| Besaran | Satuan British |
| Panjang | foot (kaki) , mil |
| massa | slug |
| Gaya | pound (lb) |
| Usaha | ft.lb |
| Daya | ft.lb/sec |
Besaran pokok dan turunan
14.15
Diposting oleh Melany Christy
Besaran merupakan segala sesuatu yang dapat diukur dan dinyatakan dengan angka, misalnya panjang, massa, waktu, luas, berat, volume, kecepatan, dll. Warna, indah, cantik, bukan merupakan besaran karena tidak dapat diukur dan dinyatakan dengan angka. Besaran dibagi menjadi dua yaitu besaran pokok dan besaran turunan.
BESARAN POKOK
Besaran Pokok adalah besaran yang satuannya telah ditetapkan terlebih dahulu dan tidak diturunkan dari besaran lain. Ada tujuh besaran pokok dalam sistem Satuan Internasional yaitu Panjang, Massa, Waktu, Suhu, Kuat Arus, Jumlah molekul, Intensitas Cahaya.
Panjang adalah dimensi suatu benda yang menyatakan jarak antar ujung. Panjang dapat dibagi menjadi tinggi, yaitu jarak vertikal, serta lebar, yaitu jarak dari satu sisi ke sisi yang lain, diukur pada sudut tegak lurus terhadap panjang benda. Dalam ilmu fisika dan teknik, kata “panjang” biasanya digunakan secara sinonim dengan “jarak”, dengan simbol “l” atau “L” (singkatan dari bahasa Inggris length).
Massa adalah sifat fisika dari suatu benda, yang secara umum dapat digunakan untuk mengukur banyaknya materi yang terdapat dalam suatu benda. Massa merupakan konsep utama dalam mekanika klasik dan subyek lain yang berhubungan.
Waktu menurut Kamus Besar Bahasa Indonesia (1997) adalah seluruh rangkaian saat ketika proses, perbuatan atau keadaan berada atau berlangsung. Dalam hal ini, skala waktu merupakan interval antara dua buah keadaan/kejadian, atau bisa merupakan lama berlangsungnya suatu kejadian. Tiap masyarakat memilki pandangan yang relatif berbeda tentang waktu yang mereka jalani. Sebagai contoh: masyarakat Barat melihat waktu sebagai sebuah garis lurus (linier). Konsep garis lurus tentang waktu diikuti dengan terbentuknya konsep tentang urutan kejadian. Dengan kata lain sejarah manusia dilihat sebagai sebuah proses perjalanan dalam sebuah garis waktu sejak zaman dulu, zaman sekarang dan zaman yang akan datang. Berbeda dengan masyarakat Barat, masysrakat Hindu melihat waktu sebagai sebuah siklus yang terus berulang tanpa akhir.
Suhu menunjukkan derajat panas benda. Mudahnya, semakin tinggi suhu suatu benda, semakin panas benda tersebut. Secara mikroskopis, suhu menunjukkan energi yang dimiliki oleh suatu benda. Setiap atom dalam suatu benda masing-masing bergerak, baik itu dalam bentuk perpindahan maupun gerakan di tempat berupa getaran. Makin tingginya energi atom-atom penyusun benda, makin tinggi suhu benda tersebut.
Arus listrik adalah banyaknya muatan listrik yang mengalir tiap satuan waktu. Muatan listrik bisa mengalir melalui kabel atau penghantar listrik lainnya. Pada zaman dulu, Arus konvensional didefinisikan sebagai aliran muatan positif, sekalipun kita sekarang tahu bahwa arus listrik itu dihasilkan dari aliran elektron yang bermuatan negatif ke arah yang sebaliknya.
Jumlah molekul
Intensitas Cahaya
BESARAN TURUNAN
Besaran turunan adalah besaran yang satuannya diturunkan dari besaran pokok atau besaran yang didapat dari penggabungan besaran-besaran pokok. Contoh besaran turunan adalah Berat, Luas, Volume, Kecepatan, Percepatan, Massa Jenis, Berat jenis, Gaya, Usaha, Daya, Tekanan, Energi Kinetik, Energi Potensial, Momentum, Impuls, Momen inersia, dll. Dalam fisika, selain tujuh besaran pokok yang disebutkan di atas, lainnya merupakan besaran turunan. Besaran Turunan selengkapnya akan dipelajari pada masing-masing pokok bahasan dalam pelajaran fisika.
Untuk lebih memperjelas pengertian besaran turunan, perhatikan beberapa besaran turunan yang satuannya diturunkan dari satuan besaran pokok berikut ini.
Luas = panjang x lebar
= besaran panjang x besaran panjang
= m x m
= m2
Volume = panjang x lebar x tinggi
= besaran panjang x besaran panjang x besaran Panjang
= m x m x m
= m3
Kecepatan = jarak / waktu
= besaran panjang / besaran waktu
= m / s
Penjumlahan Vektor
03.20
Diposting oleh Melany Christy
selisih dua buah vektor dengan metode segitiga
Misalkan dua orang anak mendorong sebuah benda dengan vektor gaya masing-masing sebesar F1 dan F2, seperti ditunjukkan diagram di bawah. Ke arah mana benda itu akan pindah ? tentu saja benda tersebut tidak berpindah searah F1 atau F2. dalam kasus seperti itu, maka benda tersebut berpindah searah dengan F1 + F2. Operasi ini disebut jumlah vektor.
Cara menggambar jumlah dua buah vektor adalah dengan metode segitiga. Pertama, gambar vektor F1 berupa tanda panah. kedua, gambar vektor kedua, F2, dengan pangkalnya berhimpitan dengan ujung vektor pertama, F1. ketiga, jumlahkan kedua vektor, dengan menggambar vektor resultan (F1 + F2), dari pangkal vektor F1 menuju ujung vektor F2. selesai. Proses ini ditunjukkan pada gambar di bawah ini.
Cara menggambar selisih vektor pada dasarnya sama dengan menggambar penjumlahan dua vektor. Sebagai contoh, sebuah vektor F1 dan vektor F2 nilainya seperti tampak pada diagram di bawah. Berapa selisih kedua vektor tersebut ? misalnya F3 adalah selisih vektor F1 dan F2, maka dapat kita tulis F3 = F1 – F2 atau F3 = F1 + (-F2). Hal ini menunjukkan bahwa selisih antara vektor F1 dan F2 sama saja dengan penjumlahan vektor F1 dan vektor -F2. tanda minus hanya menunjukkan bahwa arah -F2 berlawanan dengan F2. Bingung ? silahkan baca terus biar paham.
Bagaimana menggambar selisih vektor F1 dan F2 ?
Pertama, gambar terlebih dahulu tanda panah yang melambangkan vektor F1. kedua, gambar vektor -F2. vektor -F2 besarnya sama dengan F2, hanya arahnya berlawanan. (Lihat dan bandingkan gambar di bawah dan di atas). Ketiga, gambar tanda panah vektor resultan F3, di mana pangkal vektor F3 berimpit dengan pangkal vektor F1 dan ujung vektor F3 berimpit dengan ujung vektor -F2. Berimpit itu artinya menempel, atau apalah terserah kamu. Selesai….
Gampang to ? masih ga mudeng ? ulangi dari awal, bacanya pelan2 biar ngerti. Kalau sudah paham, lanjut, next mission…..
Menggambar Penjumlahan lebih dari 2 Vektor dengan metode Poligon
Poligon itu artinya segi banyak/banyak segi. Gimana, dah siap belum ? sekarang tarik napas panjang….
Sebelumnya, kita belajar menggambar 2 vektor dengan cara segitiga. Bagaimana jika kamu disuruh menggambar resultan atau jumlah vektor yang lebih dari 3 ?
Misalnya kamu berpindah sejauh 4 meter, vektor A (lihat gambar di bawah), lalu kamu berpindah lagi sejauh 3 meter, vektor B. Karena hobimu jalan-jalan, maka kamu pindah lagi sejauh 2 meter, vektor C. karena suka jalan-jalan maka kamu dihukum pacarmu (aneh ya…) untuk menggambar vektor perpindahanmu tadi. Loncat ke bawah….
untuk menggambar vektor resultan/hasil penjumlahan lebih dari 2 vektor, maka kamu tidak bisa menggunakan metode/cara segitiga. Kenapa? Cari tahu sendiri ya, kan dah besar. Kamu harus menggunakan metode poligon/segi banyak. Caranya, pertama, gambar vektor A. kedua, gambar vektor B, di mana pangkal vektor B berimpit/nempel dengan ujung vektor A (lihat gambar di bawah). Ketiga, gambar vektor C di ujung vektor B. caranya seperti menggambar vektor B. terakhir, gambar vektor D sebagai vektor resultan/hasil, dimana pangkal vektor D nempel dengan pangkal vektor A dan ujung vektor B nempel dengan ujung vektor C. selesai…
Kalo masih bingung, baca, sambil lihat gambar. Guampang to ? mission complete… lanjut.
Menggambar Penjumlahan 2 atau Lebih vektor dengan metode Jajaran Genjang.
Selain menggambar penjumlahan vektor dengan metode/cara segitiga dan poligon, kita juga bisa menggunakan metode jajaran genjong, eh genjang. Kalau metode segitiga khusus untuk dua vektor dan metode poligon khusus untuk lebih dari dua vektor, maka metode jajaran genjang untuk menggambar penjumlahan dua vektor atau lebih. Bagaimana menggambar penjumlahan dua vektor atau lebih menggunakan cara jajaran genjang ?
Menggambar penjumlahan 2 vektor menggunakan metode jajaran genjong.
Misalkan dua orang anak mendorong sebuah benda dengan vektor Gaya masing-masing sebesar F1 dan F2, seperti ditunjukkan diagram di bawah. Ke arah mana benda itu akan pindah ?
untuk menggambar penjumlahan dua vektor, lakukan sesuai langkah2 di bawah ini. Pertama, gambar vektor F1 menggunakan tandah panah (lihat gambar di bawah). Kedua, gambar vektor F2, di mana pangkal/buntut berimpit/nempel dengan pangkal/buntut vektor F1. ketiga, gambar vektor resultan, F3 (F1 + F2), di mana pangkal vektor F3 nempel dengan pangkal vektor F1 dan F2, sedangkan ujung vektor F3 nempel dengan titik temu garis putus-putus dari kedua ujung vektor F1 dan vektor F2 (sambil lihat gambar, biar tidak bingung).
Menggambar penjumlahan lebih dari 2 vektor menggunakan metode jajaran genjong.
Misalnya kamu berpindah sejauh 4 meter seperti vektor A (lihat gambar di bawah), lalu kamu berpindah lagi sejauh 3 meter seperti vektor B. Karena hobimu jalan-jalan, maka kamu pindah lagi sejauh 2 meter seperti vektor C. karena suka jalan-jalan maka kamu dihukum pacarmu (aneh ya…) untuk menggambar vektor perpindahanmu, tapi kali ini dengan metode jajaran genjong. Bagaimanakah ?
Untuk menggambar penjumlahan lebih dari 2 vektor, lihat petunjuk berikut ini. Pertama, gambar vektor A menggunakan tandah panah (lihat gambar di bawah). Kedua, gambar vektor B, di mana pangkalnya berimpit/nempel dengan pangkal/buntut vektor A. ketiga, gambar vektor C, di mana pangkalnya berhimpit dengan pangkal vektor A dan B. keempat, buat garis putus-putus tegak lurus dari ujung vektor A dan B sampai kedua garis putus-putus tersebut bertemu, Vektor D (buat garis satu2, kalo kamu kidal+, pake aja dua tanganmu sekalian, hehe…). Kelima, tarik garis dari pangkal vektor A,B dan C menuju titik temu garis putus-putus yang sudah kamu buat tadi (jangan lupa lihat gambar ya). Keenam, buat lagi garis putus2 tegak lurus dari titik temu vektor A dan B dan dari ujung vektor C sampai kedua garis putus2 tersebut bertemu. Nah, sekarang tarik garis lurus dari pangkal vektor A, B dan C menuju titik temu garis putus2 yang baru saja kamu buat, Vektor Resultan (R). Garis terakhir tersebut adalah vektor resultannya….
Tadi kita belajar menggambar resultan penjumlahan vektor, sekarang kita belajar menentukan besar dan arah vektor resultan.
Menentukan vektor resultan
03.11
Diposting oleh Melany Christy
MENENTUKAN VEKTOR RESULTAN DENGAN METODE GRAFIS
Dengan menggunakan metode segitiga dan poligon, kita dapat melukis vektor resultan dari dua buah vektor atau lebih. Dari gambar vektor resultan tersebut, kita dapat menentukan besar dan arah vektor resultan dengan melakukan pengukuran (bukan menghitung). Cara menentukan vektor resultan seperti ini disebut metode grafis. Sekarang, bagaimana menentukan vektor resultan dengan metode grafis ? di baca terus ya, hehe….
Langkah-langkah menentukan besar dan arah vektor resultan dengan metode grafis, adalah sebagai berikut :
- tetapkan sumbu X positif sebagai acuan menentukan arah. Ingat, sudut positif diukur dengan arah berlawanan arah jarum jam, sedangkan sudut negatif diukur dengan arah searah jarum jam.
- gambar setiap vektor yang akan dijumlahkan (lihat kembali menggambar penjumlahan vektor menggunakan jajaran genjang)
- Arah vektor digambar terhadap sumbu x positif dengan menggunakan busur derajat
Perkalian Titik dan Perkalian Silang
03.02
Diposting oleh Melany Christy
Misalnya terdapat dua vektor, yakni A dan B. Perkalian skalar dari vektor A dan B dinyatakan dengan A.B (karena digunakan notasi titik maka perkalian ini dinamakan perkalian titik). Perkalian vektor dari A dan B dinyatakan dengan A x B. Karena digunakan notasi x, maka perkalian ini disebut perkalian silang.
Perkalian titik
Misalnya diketahui vektor A dan B sebagaimana tampak pada gambar di bawah. Perkalian titik antara vektor A dan B dituliskan sebagai A.B (A titik B).
Untuk mendefinisikan perkalian titik dari vektor A dan B (A.B), digambarkan vektor A dan vektor B yang membentuk sudut teta (sambil lihat gambar di bawah). Selanjutnya kita gambarkan proyeksi dari vektor B terhadap arah vektor A. Proyeksi ini adalah komponen dari vektor B yang sejajar dengan vektor A, yang besarnya sama dengan B cos teta.
Dengan demikian, kita definisikan A.B sebagai besar vektor A yang dikalikan dengan komponen vektor B yang sejajar dengan A. Secara matematis dapat kita tulis sebagai berikut :
AB cos teta merupakan bilangan biasa (skalar). Karenanya perkalian titik disebut juga perkalian skalar. Bagaimana jika perkalian titik antara vektor A dan B dibalik menjadi B.A ? sebelum kita definisikan B.A, terlebih dahulu kita gambarkan proyeksi dari vektor A terhadap vektor B (lihat gambar di bawah).
Berdasarkan gambar ini, kita dapat mendefinisikan B.A sebagai besar vektor B yang dikalikan dengan komponen vektor A yang sejajar dengan B. Secara matematis dapat kita tulis sebagai berikut :
Hasil perkalian titik A.B = AB cos teta dan hasil perkalian titik B.A = BA cos teta. Karena AB cos teta = BA cos teta, maka berlaku A.B = B.A
Beberapa hal dalam perkalian titik yang perlu anda ketahui :
1. Perkalian titik memenuhi hukum komutatif
A.B = B.A
2. Perkalian titik memenuhi hukum distributif
A. (B + C) = A.B + A.C
3. Jika vektor A dan B saling tegak lurus, maka hasil perkalian titik A.B = 0
Ketika vektor A dan B saling tegak lurus, maka sudut yang dibentuk adalah 90o. Cos 90o = 0. Dengan demikian : A.B = AB cos teta = AB cos 90o = 0. Sebaliknya, B.A = BA cos teta = BA cos 90o = 0
4. Jika vektor A dan vektor B searah, maka A.B = AB cos 0o = AB
Ketika vektor A dan B searah, maka sudut yang dibentuk adalah 0o. Cos 0 = 1. Dengan demikian, A.B = AB cos teta = AB cos 0o = AB. Sebaliknya B.A = BA cos teta = BA cos 0o = BA
(Anda jangan bingung dengan AB dan BA. Besar AB = besar BA. Misalnya besar vektor A = 2. besar vektor B = 3. maka A.B = 2.3 = 6; ini sama saja dengan B.A = 3.2 = 6. dipahami perlahan-lahan ya…)
5. Syarat lain dari dua vektor yang searah, jika A = B maka diperoleh A.A = A2 atau B.B = B2
6. Jika vektor A dan B berlawanan arah (ketika dua vektor berlawanan arah maka sudut yang dibentuk adalah 180º), maka hasil perkalian A.B = AB cos 180º = AB (-1) = -AB.
Cos 180º = -1.
Contoh soal :
Sebuah vektor A memiliki besar 4 satuan dan vektor B memiliki 3 satuan. Tentukan hasil perkalian titik dari kedua vektor jika sudut yang dibentuk oleh kedua vektor adalah 60º, 90º dan 180o
Panduan jawaban :
Karena A.B = B.A maka kita bisa memilih menggunakan salah satu. Misalnya kita menggunakan A.B, dengan demikian kita tulis persamaannya
A.B = AB cos teta
Besar A = 4 satuan dan besar B = 3 satuan.
Soal latihan :
Dua vektor A dan B masing-masing besarnya 6 satuan dan 4 satuan. Tentukan perkalian titik antara kedua vektor jika sudut yang terbentuk adalah 30o, 60o, 90o, 120o, 150o, 180o
Perkalian silang
Perkalian silang dari dua vektor, misalnya vektor A dan B ditulis sebagai A x B (A silang B). Perkalian silang dikenal dengan julukan perkalian vektor, karena hasil perkalian ini menghasilkan besaran vektor.
Misalnya vektor A dan vektor B tampak seperti gambar di bawah.
Untuk mendefinisikan perkalian silang antara vektor A dan B (A x B), kita gambarkan vektor A dan B seperti gambar di atas, dan digambarkan juga komponen vektor B yang tegak lurus pada A (lihat gambar di bawah), yang besarnya sama dengan B sin teta
Dengan demikian, kita dapat mendefinisikan besar perkalian silang vektor A dan B (A x B) sebagai hasil kali besar vektor A dengan komponen vektor B yang tegak lurus pada vektor A.
Bagaimana jika A x B kita balik menjadi B x A ?
Terlebih dahulu kita gambarkan vektor B dan A serta komponen vektor A yang tegak lurus pada B (amati gambar di bawah…)
Berdasarkan gambar ini, kita dapat mendefinisikan perkalian silang antara vektor B dan A (B x A) sebagai hasil kali besar vektor B dengan komponen vektor A yang tegak lurus pada vektor B. Secara matematis ditulis :
Arah Perkalian Silang A x B
Perkalian silang adalah perkalian vektor, sehingga hasil perkaliannya memiliki besar dan arah. Besar hasil perkalian vektor telah kita turunkan di atas, sekarang kita menentukan arahnya. Untuk menentukan arah A x B, terlebih dahulu kita gambarkan vektor A dan B seperti gambar di bawah. Kedua vektor ini kita letakan pada suatu bidang (sambil lihat gambar di bawah ya….)
Kita definisikan perkalian silang A x B sebagai suatu vektor yang tegak lurus bidang di mana vektor A dan B berada. Besarnya sama dengan AB sin teta. Jika C = A x B maka C = AB sin teta
Arah C tegak lurus bidang di mana vektor A dan B berada. Kita dapat menggunakan kaidah tangan kanan untuk menentukan arah C. Jika kita menggenggam jari tangan di mana arahnya berlawanan dengan arah putaran jarum jam, maka arah C searah dengan arah ibu jari menuju ke atas.
Arah Perkalian Silang B x A
Untuk menentukan arah B x A, terlebih dahulu kita gambarkan vektor B dan A seperti gambar di bawah. Kedua vektor ini kita letakan pada suatu bidang (sambil lihat gambar di bawah ya….)
Jika C = B x A maka C = BA sin teta.
Arah C tegak lurus bidang di mana vektor B dan A berada. Kita dapat menggunakan kaidah tangan kanan untuk menentukan arah C. Jika kita menggenggam jari tangan di mana arahnya searah dengan arah putaran jarum jam, maka arah C sama dengan arah ibu jari menuju ke bawah.
A x B tidak sama dengan B x A. Hasil perkalian silang menghasilkan besaran vektor, di mana selain mempunyai besar, juga mempunyai arah. Pada penurunan di atas, arah A x B berlawanan arah dengan B x A.
Beberapa hal dalam perkalian silang yang perlu anda ketahui :
1. Perkalian silang bersifat anti komutatif.
A x B = – B x A
Tanda negatif menunjukkan bahwa arah B pada A x B berlawanan dengan arah B pada B x A.
2. Jika kedua vektor saling tegak lurus maka sudut yang dibentuk adalah 90o. Sin 90o = 1. Dengan demikian, besar hasil perkalian silang antara vektor A dan B akan tampak sebagai berikut :
A x B = AB sin teta = AB sin 90o = AB
B x A = BA sin teta = BA sin 90o = BA
Ingat ya, ini adalah besar hasil perkalian silang.
3. Jika kedua vektor searah, maka sudut yang dibentuk adalah 0o. Namanya juga segaris…
Sin 0o = 0. Dengan demikian, nilai alias besar hasil perkalian silang antara vektor A dan B akan tampak sebagai berikut.
A x B = AB sin teta = AB sin 0o = 0
B x A = BA sin teta = BA sin 0o = 0
Hasil perkalian silang antara dua vektor yang searah alias segaris kerja sama dengan n0L.
Referensi
Giancoli, Douglas C., 2001, Fisika Jilid I (terjemahan), Jakarta : Penerbit Erlangga
Halliday dan Resnick, 1991, Fisika Jilid I, Terjemahan, Jakarta : Penerbit Erlangga
Tipler, P.A.,1998, Fisika untuk Sains dan Teknik-Jilid I (terjemahan), Jakarta : Penebit Erlangga
Young, Hugh D. & Freedman, Roger A., 2002, Fisika Universitas (terjemahan), Jakarta : Penerbit Erlangga
Sumber : http://www.gurumuda.com/perkalian-titik-dan-perkalian-silang/






























