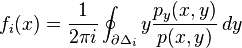Algebraic function
19.56
Diposting oleh Melany Christy
In mathematics, an algebraic function is informally a function which satisfies a polynomial equation whose coefficients are themselves polynomials. For example, an algebraic function in one variable x is a solution y for an equation
where the coefficients ai(x) are polynomial functions of x. A function which is not algebraic is called a transcendental function.
In more precise terms, an algebraic function may not be a function at all, at least not in the conventional sense. Consider for example the equation of a circle:
This determines y, except only up to an overall sign:
However, both branches are thought of as belonging to the "function" determined by the polynomial equation. Thus an algebraic function is most naturally considered as a multiple valued function.
An algebraic function in n variables is similarly defined as a function y which solves a polynomial equation in n + 1 variables:
It is normally assumed that p should be an irreducible polynomial. The existence of an algebraic function is then guaranteed by the implicit function theorem.
Formally, an algebraic function in n variables over the field K is an element of the algebraic closure of the field of rational functions K(x1,...,xn). In order to understand algebraic functions as functions, it becomes necessary to introduce ideas relating to Riemann surfaces or more generally algebraic varieties, and sheaf theory.
Introduction and overview
The informal definition of an algebraic function provides a number of clues about the properties of algebraic functions. To gain an intuitive understanding, it may be helpful to regard algebraic functions as functions which can be formed by the usual algebraic operations: addition, multiplication, division, and taking an nth root. Of course, this is something of an oversimplification; because of casus irreducibilis (and more generally the fundamental theorem of Galois theory), algebraic functions need not be expressible by radicals.
First, note that any polynomial is an algebraic function, since polynomials are simply the solutions for y of the equation
More generally, any rational function is algebraic, being the solution of
Moreover, the nth root of any polynomial is an algebraic function, solving the equation
Surprisingly, the inverse function of an algebraic function is an algebraic function. For supposing that y is a solution of
for each value of x, then x is also a solution of this equation for each value of y. Indeed, interchanging the roles of x and y and gathering terms,
Writing x as a function of y gives the inverse function, also an algebraic function.
However, not every function has an inverse. For example, y = x2 fails the horizontal line test: it fails to be one-to-one. The inverse is the algebraic "function"  . In this sense, algebraic functions are often not true functions at all, but instead are multiple valued functions.
. In this sense, algebraic functions are often not true functions at all, but instead are multiple valued functions.
Another way to understand this, which will become important later in the article, is that an algebraic function is the graph of an algebraic curve.
The role of complex numbers
From an algebraic perspective, complex numbers enter quite naturally into the study of algebraic functions. First of all, by the fundamental theorem of algebra, the complex numbers are an algebraically closed field. Hence any polynomial relation
- p(y, x) = 0
is guaranteed to have at least one solution (and in general a number of solutions not exceeding the degree of p in x) for y at each point x, provided we allow y to assume complex as well as real values. Thus, problems to do with the domain of an algebraic function can safely be minimized.

Furthermore, even if one is ultimately interested in real algebraic functions, there may be no adequate means to express the function in a simple manner without resorting to complex numbers (see casus irreducibilis). For example, consider the algebraic function determined by the equation
Using the cubic formula, one solution is (the red curve in the accompanying image)
There is no way to express this function in terms of real numbers only, even though the resulting function is real-valued on the domain of the graph shown.
On a more significant theoretical level, using complex numbers allow one to use the powerful techniques of complex analysis to discuss algebraic functions. In particular, the argument principle can be used to show that any algebraic function is in fact an analytic function, at least in the multiple-valued sense.
Formally, let p(x, y) be a complex polynomial in the complex variables x and y. Suppose that x0 ∈ C is such that the polynomial p(x0,y) of y has n distinct zeros. We shall show that the algebraic function is analytic in a neighborhood of x0. Choose a system of n non-overlapping discs Δi containing each of these zeros. Then by the argument principle
By continuity, this also holds for all x in a neighborhood of x0. In particular, p(x,y) has only one root in Δi, given by the residue theorem:
which is an analytic function.
Monodromy
Note that the foregoing proof of analyticity derived an expression for a system of n different function elements fi(x), provided that x is not a critical point of p(x, y). A critical point is a point where the number of distinct zeros is smaller than the degree of p, and this occurs only where the highest degree term of p vanishes, and where the discriminant vanishes. Hence there are only finitely many such points c1, ..., cm.
A close analysis of the properties of the function elements fi near the critical points can be used to show that the monodromy cover is ramified over the critical points (and possibly the point at infinity). Thus the entire function associated to the fi has at worst algebraic poles and ordinary algebraic branchings over the critical points.
Note that, away from the critical points, we have
since the fi are by definition the distinct zeros of p. The monodromy group acts by permuting the factors, and thus forms the monodromy representation of the Galois group of p. (The monodromy action on the universal covering space is related but different notion in the theory of Riemann surfaces.)
History
The ideas surrounding algebraic functions go back at least as far as René Descartes. The first discussion of algebraic functions appears to have been in Edward Waring's 1794 An Essay on the Principles of Human Knowledge in which he writes:
- let a quantity denoting the ordinate, be an algebraic function of the abscissa x, by the common methods of division and extraction of roots, reduce it into an infinite series ascending or descending according to the dimensions of x, and then find the integral of each of the resulting terms.
Algebraic extension
19.53
Diposting oleh Melany Christy
For example, the field extension R/Q, that is the field of real numbers as an extension of the field of rational numbers, is transcendental, while the field extensions C/R and Q(√2)/Q are algebraic, where C is the field of complex numbers.
All transcendental extensions are of infinite degree. This in turn implies that all finite extensions are algebraic[1]. The converse is not true however: there are infinite extensions which are algebraic. For instance, the field of all algebraic numbers is an infinite algebraic extension of the rational numbers.
If a is algebraic over K, then K[a], the set of all polynomials in a with coefficients in K, is not only a ring but a field: an algebraic extension of K which has finite degree over K. In the special case where K = Q is the field of rational numbers, Q[a] is an example of an algebraic number field.
A field with no proper algebraic extensions is called algebraically closed. An example is the field of complex numbers. Every field has an algebraic extension which is algebraically closed (called its algebraic closure), but proving this in general requires some form of the axiom of choice.
An extension L/K is algebraic if and only if every sub K-algebra of L is a field.
Generalizations
Model theory generalizes the notion of algebraic extension to arbitrary theories: an embedding of M into N is called an algebraic extension if for every x in N there is a formula p with parameters in M, such that p(x) is true and the set
- {y in N | p(y)}
is finite. It turns out that applying this definition to the theory of fields gives the usual definition of algebraic extension. The Galois group of N over M can again be defined as the group of automorphisms, and it turns out that most of the theory of Galois groups can be developed for the general case.
Algebraic element
19.52
Diposting oleh Melany Christy
In mathematics, if L is a field extension of K, then an element a of L is called an algebraic element over K, or just algebraic over K, if there exists some non-zero polynomial g(x) with coefficients in K such that g(a)=0. Elements of L which are not algebraic over K are called transcendental over K.
These notions generalize the algebraic numbers and the transcendental numbers (where the field extension is C/Q, C being the field of complex numbers and Q being the field of rational numbers).
Examples
- The square root of 2 is algebraic over Q, since it is the root of the polynomial g(x) = x2 - 2 whose coefficients are rational.
- Pi is transcendental over Q but algebraic over the field of real numbers R: it is the root of g(x) = x - π, whose coefficients (1 and -π) are both real, but not of any polynomial with only rational coefficients. (The definition of the term transcendental number uses C/Q, not C/R.)
Properties
The following conditions are equivalent for an element a of L:
- a is algebraic over K
- the field extension K(a)/K has finite degree, i.e. the dimension of K(a) as a K-vector space is finite. (Here K(a) denotes the smallest subfield of L containing K and a)
- K[a] = K(a), where K[a] is the set of all elements of L that can be written in the form g(a) with a polynomial g whose coefficients lie in K.
This characterization can be used to show that the sum, difference, product and quotient of algebraic elements over K are again algebraic over K. The set of all elements of L which are algebraic over K is a field that sits in between L and K.
If a is algebraic over K, then there are many non-zero polynomials g(x) with coefficients in K such that g(a) = 0. However there is a single one with smallest degree and with leading coefficient 1. This is the minimal polynomial of a and it encodes many important properties of a.
Fields that do not allow any algebraic elements over them (except their own elements) are called algebraically closed. The field of complex numbers is an example.
Algebraic solution
19.50
Diposting oleh Melany Christy
The solution of an algebraic equation, often one that seeks zeros of a polynomial, is sometimes said to admit an "algebraic solution" or a "solution in radicals" if function that expresses the solution in terms of the coefficients relies only on addition, subtraction, multiplication, division, and the extraction of roots. The most well-known example is the solution
introduced in secondary school, of the quadratic equation
(where a ≠ 0).
The Abel-Ruffini theorem states that the general quintic equation lacks an algebraic solution.
An algebraic solution is not the same thing as a closed-form expression.
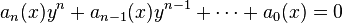




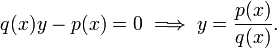
![y^n-p(x)=0 \implies y=\sqrt[n]{p(x)}.](http://upload.wikimedia.org/math/0/e/6/0e6043dc7717cca9ba05d5567366478e.png)


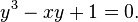
![y=-\frac{(1+i\sqrt{3})x}{2^{2/3}\sqrt[3]{729-108x^3}}-\frac{(1-i\sqrt{3})\sqrt[3]{-27+\sqrt{729-108x^3}}}{6\sqrt[3]{2}}.](http://upload.wikimedia.org/math/3/3/6/3369bbe90a387b41bbe25214063abb56.png)