Binary operation
16.21
Diposting oleh Melany Christy
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division.
More precisely, a binary operation on a set S is a ternary relation that maps elements of the Cartesian product S × S to S:
If f is not a function, but is instead a partial function, it is called a partial operation. For instance, division of real numbers is a partial function, because one can't divide by zero: a/0 is not defined for any real a. Note however that both in algebra and model theory the binary operations considered are defined on the whole of  .
.
Sometimes, especially in computer science, the term is used for any binary function. That f takes values in the same set S that provides its arguments is the property of closure.
Binary operations are the keystone of algebraic structures studied in abstract algebra: they form part of groups, monoids, semigroups, rings, and more. Most generally, a magma is a set together with any binary operation defined on it.
Many binary operations of interest in both algebra and formal logic are commutative or associative. Many also have identity elements and inverse elements. Typical examples of binary operations are the addition (+) and multiplication (×) of numbers and matrices as well as composition of functions on a single set.
An example of an operation that is not commutative is subtraction (−). Examples of partial operations that are not commutative include division (/), exponentiation(^), and super-exponentiation(↑↑).
Binary operations are often written using infix notation such as a ∗ b, a + b, a · b or (by juxtaposition with no symbol) ab rather than by functional notation of the form f(a, b). Powers are usually also written without operator, but with the second argument as superscript.
Binary operations sometimes use prefix or postfix notation; this dispenses with parentheses. Prefix notation is also called Polish notation; postfix notation, also called reverse Polish notation, is probably more often encountered.
Pair and tuple
A binary operation, ab, depends on the ordered pair (a, b) and so (ab)c (where the parentheses here mean first operate on the ordered pair (a, b) and then operate on the result of that using the ordered pair ((ab), c)) depends in general on the ordered pair ((a,b),c). Thus, for the general, non-associative case, binary operations can be represented with binary trees.
However:
- If the operation is associative, (ab)c=a(bc), then the value depends only on the tuple (a,b,c).
- If the operation is commutative, ab=ba, then the value depends only on the multiset { {a,b},c}.
- If the operation is both associative and commutative then the value depends only on the multiset {a,b,c}.
- If the operation is both associative and commutative and idempotent, aa=a, then the value depends only on the set {a,b,c}.
External binary operations
An external binary operation is a binary function from K × S to S. This differs from a binary operation in the strict sense in that K need not be S; its elements come from outside.
An example of an external binary operation is scalar multiplication in linear algebra. Here K is a field and S is a vector space over that field.
An external binary operation may alternatively be viewed as an action; K is acting on S.
Note that the dot product of two vectors is not a binary operation, external or otherwise, as it maps from S × S to K, where K is a field and S is a vector space over K.
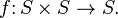

Posting Komentar