Inverse trigonometric functions
06.27
Diposting oleh Melany Christy
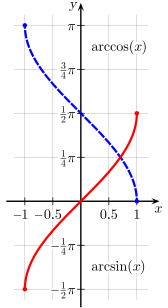
In mathematics, the inverse trigonometric functions or cyclometric functions are the so-called inverse functions of the trigonometric functions, though they do not meet the official definition for inverse functions as their ranges are subsets of the domains of the original functions. Since none of the six trigonometric functions are one-to-one (by failing the horizontal line test), they must be restricted in order to have inverse functions.
For example, just as the square root function  is defined such that y2 = x, the function y = arcsin(x) is defined so that sin(y) = x. There are multiple numbers y such that sin(y) = x; for example, sin(0) = 0, but also sin(π) = 0, sin(2π) = 0, etc. It follows that the arcsine function is multivalued: arcsin(0) = 0, but also arcsin(0) = π, arcsin(0) = 2π, etc. When only one value is desired, the function may be restricted to its principal branch. With this restriction, for each x in the domain the expression arcsin(x) will evaluate only to a single value, called its principal value. These properties apply to all the inverse trigonometric functions.
is defined such that y2 = x, the function y = arcsin(x) is defined so that sin(y) = x. There are multiple numbers y such that sin(y) = x; for example, sin(0) = 0, but also sin(π) = 0, sin(2π) = 0, etc. It follows that the arcsine function is multivalued: arcsin(0) = 0, but also arcsin(0) = π, arcsin(0) = 2π, etc. When only one value is desired, the function may be restricted to its principal branch. With this restriction, for each x in the domain the expression arcsin(x) will evaluate only to a single value, called its principal value. These properties apply to all the inverse trigonometric functions.
The principal inverses are listed in the following table.
| Name | Usual notation | Definition | Domain of x for real result | Range of usual principal value
(radians) | Range of usual principal value
(degrees) |
|---|---|---|---|---|---|
| arcsine | y = arcsin x | x = sin y | −1 ≤ x ≤ 1 | −π/2 ≤ y ≤ π/2 | −90° ≤ y ≤ 90° |
| arccosine | y = arccos x | x = cos y | −1 ≤ x ≤ 1 | 0 ≤ y ≤ π | 0° ≤ y ≤ 180° |
| arctangent | y = arctan x | x = tan y | all real numbers | −π/2 < y < π/2 | −90° < y <> |
| arccotangent | y = arccot x | x = cot y | all real numbers | 0 < y < π | 0° < y <> |
| arcsecant | y = arcsec x | x = sec y | x ≤ −1 or 1 ≤ x | 0 ≤ y < π/2 or π/2 < y ≤ π | 0° ≤ y <>y ≤ 180° |
| arccosecant | y = arccsc x | x = csc y | x ≤ −1 or 1 ≤ x | −π/2 ≤ y <>y ≤ π/2 | -90° ≤ y <>y ≤ 90° |
If x is allowed to be a complex number, then the range of y applies only to its real part.
The notations sin−1, cos−1, etc. are often used for arcsin, arccos, etc., but this convention logically conflicts with the common semantics for expressions like sin2(x), which refer to numeric power rather than function composition, and therefore may result in confusion between multiplicative inverse and compositional inverse.
In computer programming languages the functions arcsin, arccos, arctan, are usually called asin, acos, atan. Many programming languages also provide the two-argument atan2 function, which computes the arctangent of y / x given y and x, but with a range of (−π, π].
Relationships among the inverse trigonometric functions


Complementary angles:
Negative arguments:
Reciprocal arguments:
0 \, " src="http://upload.wikimedia.org/math/8/e/1/8e185447927c80999f60c4f352b62057.png">
0" src="http://upload.wikimedia.org/math/0/b/6/0b6c7eb2b7d0ef9b6ffa2122b165e50a.png">
If you only have a fragment of a sine table:
Whenever the square root of a complex number is used here, we choose the root with the positive real part (or positive imaginary part if the square was negative real).
From the half-angle formula  , we get:
, we get:
Relationships between trigonometric functions and inverse trigonometric functions
General solutions
Each of the trigonometric functions is periodic in the real part of its argument, running through all its values twice in each interval of 2π. Sine and cosecant begin their period at 2πk − π/2 (where k is an integer), finish it at 2πk + π/2, and then reverse themselves over 2πk + π/2 to 2πk + 3π/2. Cosine and secant begin their period at 2πk, finish it at 2πk + π, and then reverse themselves over 2πk + π to 2πk + 2π. Tangent begins its period at 2πk − π/2, finishes it at 2πk + π/2, and then repeats it (forward) over 2πk + π/2 to 2πk + 3π/2. Cotangent begins its period at 2πk, finishes it at 2πk + π, and then repeats it (forward) over 2πk + π to 2πk + 2π.
This periodicity is reflected in the general inverses:
Derivatives of inverse trigonometric functions
- Main article: Differentiation of trigonometric functions
Simple derivatives for real and complex values of x are as follows:
Only for real values of x:
1\\ \frac{d}{dx} \arccsc x & {}= \frac{-1}{|x|\,\sqrt{x^2-1}}; \qquad |x| > 1 \end{align}" src="http://upload.wikimedia.org/math/f/e/b/febfe62e8b81023b62ab0108dc26b528.png">
For a sample derivation: if 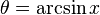 , we get:
, we get:
Expression as definite integrals
Integrating the derivative and fixing the value at one point gives an expression for the inverse trigonometric function as a definite integral:
When x equals 1, the integrals with limited domains are improper integrals, but still well-defined.
Infinite series
Like the sine and cosine functions, the inverse trigonometric functions can be calculated using infinite series, as follows:
Leonhard Euler found a more efficient series for the arctangent, which is:
(Notice that the term in the sum for n= 0 is the empty product which is 1.)
Alternatively, this can be expressed:
Continued fraction for arctangent
An alternative to the power series for arctangent is its generalized continued fraction:
This is valid in the cut complex plane. There are two cuts, from −i to the point at infinity, going down the imaginary axis, and from i to the point at infinity, going up the same axis. It works best for real numbers running from −1 to 1. The partial denominators are the odd natural numbers, and the partial numerators (after the first) are just (nz)2, with each perfect square appearing once. It was developed by Carl Friedrich Gauss, utilizing the hypergeometric series.
Indefinite integrals of inverse trigonometric functions
For real and complex values of x:
For real x ≥ 1:
All of these can be derived using integration by parts and the simple derivative forms shown above.
Example
Using  , set
, set
Then
Substitute
Then
and
Back-substitute for x to yield
Two-argument variant of arctangent
The two-argument atan2 function computes the arctangent of y / x given y and x, but with a range of (−π, π]. In other words, atan2(y, x) is the angle between the positive x-axis of a plane and the point (x, y) on it, with positive sign for counter-clockwise angles (upper half-plane, y > 0), and negative sign for clockwise angles (lower half-plane, y <>
In terms of the standard arctan function, that is with range of (−π/2, π/2), it can be expressed as follows:
0 \\ \pi + \arctan(\frac y x) & \qquad y \ge 0 , x <> 0 , x = 0 \\ -\frac{\pi}{2} & \qquad y < x =" 0" y =" 0," x =" 0" src="http://upload.wikimedia.org/math/1/4/a/14a04ec5ece69dcae0cbc0336186e026.png">
It also equals the principal value of the argument of the complex number x + iy.
This function may also be defined using the tangent half-angle formulae as follows:
provided that either x > 0 or y ≠ 0. However this fails if given x ≤ 0 and y = 0 so the expression is unsuitable for computational use.
The above argument order (y, x) seems to be the most common, and in particular is used in ISO standards such as the C programming language, but a few authors may use the opposite convention (x, y) so some caution is warranted.
Logarithmic forms
These functions may also be expressed using complex logarithms. This extends in a natural fashion their domain to the complex plane.
Elementary proofs of these relations proceed via expansion to exponential forms of the trigonometric functions.
Example proof
(exponential definition of sine)
Let
Then
(the positive branch is chosen)
Q.E.D.
 |  | 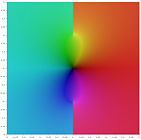 |  | 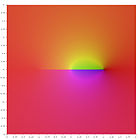 |  |
| arcsin(z) | arccos(z) | arctan(z) | arccot(z) | arcsec(z) | arccsc(z) |
Arctangent addition formula
this is derived from the tangent addition formula
Practical use
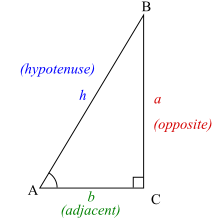
Inverse trigonometric functions are useful when trying to determine the remaining two angles of a right triangle when the lengths of the sides of the triangle are known. Recalling the right-triangle definitions of sine, for example, it follows that
Often, the hypotenuse is unknown and would need to be calculated before using arcsine or arccosine. Arctangent comes in handy in this situation, as the length of the hypotenuse is not needed.
For example, suppose a roof drops 8 feet as it runs out 20 feet. The roof makes an angle θ with the horizontal, where θ may be computed as follows:
















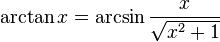














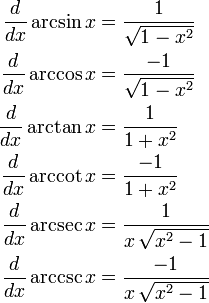


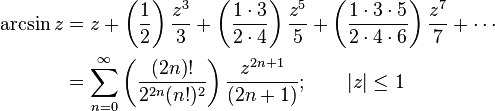






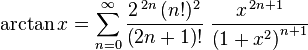





















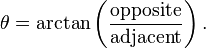


Posting Komentar