Photoelectric Effect
08.14
Diposting oleh Melany Christy
The photoelectric effect is the emission of electrons by substances, especially metals, when light falls on their surfaces.
If you illuminate a metallic surface with electromagnetic radiation that is above a threshold frequency (which is unique to the type of surface and material), the photons are absorbed and electrons are emitted from the surface . No electrons are emitted for radiation with a frequency below that of the threshold, as the electrons are unable to gain sufficient energy to overcome the electrostatic barrier of the work function of the metal.
The energy of the photon is all absorbed by the electron and if sufficient the electron can escape from the material with a finite kinetic energy made up of any energy supplied above the work function. A single photon can only eject a single electron, as the energy of one photon may only be absorbed by one electron. The electrons that are emitted are often called photoelectrons. Electrons can absorb energy from photons when irradiated, but they adhere to an "all or nothing" code of conduct. All of the energy from one photon must be absorbed and used to free one electron from atomic binding, or the energy is re-emitted. If the photon is absorbed, some of the energy is used to liberate it from the atom, and the rest contributes to the electron's kinetic (moving) energy as a free particle.
The effect was discovered by H. R. Hertz (the one that the unit of frequency is named after!) in 1887. The failure of the classical theory of electromagnetic radiation to explain it helped lead to the development of the quantum theory .
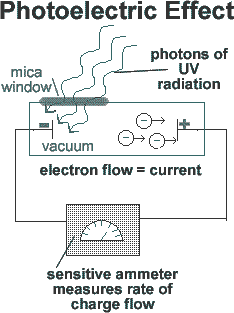 According to classical theory, when light, thought to be composed of waves, strikes substances, the energy of the liberated electrons ought to be proportional to the intensity of light. Experiments showed that, although the electron current produced depends upon the intensity of the light, the maximum energy of the electrons was not dependent on the intensity. Moreover, classical theory predicted that the photoelectric current should not depend on the frequency of the light and that there should be a time lag between the reception of light on the surface and the emission of the electrons. Neither of these predictions was borne out by experiment.
According to classical theory, when light, thought to be composed of waves, strikes substances, the energy of the liberated electrons ought to be proportional to the intensity of light. Experiments showed that, although the electron current produced depends upon the intensity of the light, the maximum energy of the electrons was not dependent on the intensity. Moreover, classical theory predicted that the photoelectric current should not depend on the frequency of the light and that there should be a time lag between the reception of light on the surface and the emission of the electrons. Neither of these predictions was borne out by experiment.
If a beam of light is pointed at the negative end of a pair of charged plates enclosed in a vacuum, a current flow is measured. Thus, the beam of light must be liberating electrons from one metal plate, which are attracted to the other plate by electrostatic forces, crossing the gap and completing the circuit. This results in a current flow.
Using the classical Maxwell wave theory of light, the more intense the incident light the greater the energy with which the electrons should be ejected from the metal. That is, the average energy carried by an ejected (photoelectric) electron should increase with the intensity of the incident light.
In fact, Lénard found that this was not so. Rather, he found the energies of the emitted electrons to be independent of the intensity of the incident radiation.
So in classical physics, one would expect the current flow to be proportional to the total amount of light energy shone onto the metal - the strength of the beam of light and the time it was shining on the plate would both play a part. But this was NOT found to be the case. It was true that the more light intensity, the more electrons were liberated and the more current was produced. However, whether the current flowed at all depended on the wavelength of the light - there was a sharp 'cut-off' wavelength above which no current at all flowed no matter how strong the beam or how long it shone for!.
In 1905 Einstein successfullly explained the photoelectric effect within the context of the new physics of the time, quantum physics. In his scientific paper, he showed that light was made of 'packets of energy' - quanta called photons. Each photon has a specific energy related to its wavelength, such that photons of short wavelength (blue light) carry more energy than long wavelength (red light) photons.
To release an electron from a metal plate required a energy above a certain value. That energy was called the 'work function energy'. It was the energy required to do work against the structure of the metal that the electron was part of. An electron on the surface of the metal (the least tightly held one in the structure) was bound to the metal by that energy and to release it you had to input that amount of energy. Each metal has a different structure and so was found to have a different 'work function'. Those that held on to their electrons lightly had low work functions those that held on tightly a high one!
The electrons could not absorb more than one photon to escape from the surface, they could not therefore absorb one quanta and then another to make up the required amount - it was as if they could only embrace one quantum at a time. If the quantum absorbed was not of sufficient energy the electron could not break free. So 'escape energy' could only be transferred by a photon of energy equal or greater than that minimum threshold energy (i.e. the wavelength of the light had to be a sufficiently short). Each photon of blue light released an electron. But all red photons were too weak. The result is no matter how much red light was shown on the metal plate, there was no current.
If the photon absorbed was of a higher energy than required just to free the electron the remainder became kinetic energy of the electron. Therefore the maximum kinetic energy of the electrons released depends on the work function ![]() of the metal and the frequency of the light shone onto it!
of the metal and the frequency of the light shone onto it!
E = hf = ![]() + Ek(MAX)
+ Ek(MAX)
This equation means that:
A photon (E = hf) absorbed by the electron (in entirety - because it cannot share its energy among several!) is used to provide energy for the electron to escape from the metal (
) and any excess energy is converted into kinetic energy.
The MAX is there because the electrons with the most energy left over for KE will be those on the surface, but some a little deeper will also escape but need to use more of the energy to do work against the metal's hold on them! So, in reality a range of energies will be observed.
![]() Sketch a graph of the kinetic energy of the 'freed' photoelectrons agains frequency using the above equation - click here for the solution.
Sketch a graph of the kinetic energy of the 'freed' photoelectrons agains frequency using the above equation - click here for the solution.
The photoelectric effect explanation earned Einstein the Nobel Prize, and first introduced the term ``photon'' of light into our terminology. - so a photon is a quantum of electromagnetic energy with energy of hf - and only one photon can be absorbed by an electron at a time.
This phenomenon could not be understood without the concept of light as being particle-like - a photon, a quantum amount of light energy for a particular frequency. If light were simple a wave-like phenomenon then increasing the intensity and thereby increasing the total energy falling on the surface would be expected to eventually provide enough energy to release electrons no matter what the frequency. Furthermore, in the classical picture one would expect the maximum energy of the emitted electrons to depend on the intensity of the light -- but it does not.
So this is evidence that light behaves as if it were a particle.
Summary of photoelectric emission
- For a given metal and frequency of incident radiation, the number of photoelectrons ejected per second is directly proportional to the intensity of the incident light.
- For a given metal, there exists a certain minimum frequency of incident radiation below which no emission of photoelectrons takes place. This frequency is called the threshold frequency.
- Above the threshold frequency, the maximum kinetic energy of the emitted photoelectron is independent of the intensity of the incident light but depends only upon the frequency (or wavelength) of the incident light.
- The time lag between the incidence of radiation and the emission of a photoelectron is very small, less then 10-9 second.
- This is evidence of the particular nature of light.

6 Maret 2010 pukul 08.44
wih hebat....
pasti yang nulis pinter nih.....
\udah ngajarin, pake english juga