What is a transformer?

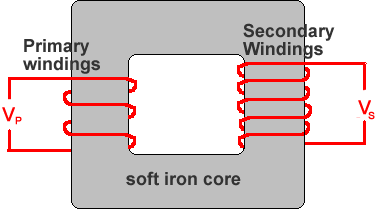
It is a laminated (made up in layers - see the photo below) soft iron core with two insulated coils of wire wrapped around it.

Click here for Faraday's early experiment

The windings of the core are made of low resistance copper. The first coil is called the primary coil. This is the coil that has the supply voltage applied across its ends. The second coil is called the secondary coil. This is the coil that has the output voltage across its ends. This is the coil that is connected to your appliance.

Why is the core laminated?

The core is not designed to have any currents induced in it. It is however a conducting loop that experiences a changing magnetic field, it will therefore have small currents induced in it - these are called 'eddy currents'. The core is laminated to reduce these to a minimum as they interfere with the efficient transfer of energy from the primary coil to the secondary one. The eddy currents cause energy to be lost from the transformer as they heat up the core. Laminated means 'made up of insulated layers of iron 'glued' together' rather than being in a single solid 'lump'. A laminated core has a higher resistance than a non-laminated one with the same number of domains. It therefore does not get such big a currents induced in it

How a transformer works

An alternating voltage (V_P) is applied across the primary coil. This causes a changing magnetic field to be formed around the primary coil.
The magnetic domains inside the soft iron core line up in response to the magnetic field from the coil.
The secondary coil experiences the changing magnetic field produced by the primary and the core. It responds to this changing magnetic field by producing a voltage (V_S) across its ends (an induced EMF) by electromagnetic induction.

(The key words you must mention when explaining this are in bold type)

Why must the source voltage be an alternating voltage?

Electromagnetic induction only happens when a wire loop experiences a changing magnetic field . The wire and field lines must move with respect to each other so that the wire can 'cut the lines of flux'.

How can we get a different voltage out of a transformer from the one we put in?

This is achieved by varying the ratio of the number of turns of wire on the primary and secondary coils. If there are more turns on the secondary then the output voltage will be bigger by the same ratio and vice versa.

A step-up transformer has more turns on the secondary than on the primary. It therefore produces a bigger output voltage than input voltage.

A step-down transformer has less turns on the secondary than on the primary. It therefore produces a smaller output voltage than input voltage.

Although transformers lose some of the energy input as heat (that is why the transformer gets warm), they are pretty efficient and about 99.9% of the input electrical energy is converted to output electrical energy. Therefore in examination questions at this level you can assume that the transformer is 100% efficient.

This means that:

power in = power out

power of primary = power of secondary

P_P = P_S

I_PV_P = I_SV_S

As the voltage is stepped up, so the current is stepped down!

In the above photograph the school transformer was used. 10.05V (rounded by the meter to 10.1V) across the primary coil of 2,000 turns resulted in an output of 100.5V across the secondary coil of 20,000 turns.

The Symbol

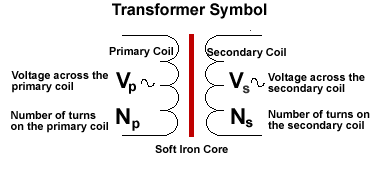
The symbol consists of two curled lines, representing the coils. These are unconnected, as there is no connection between the coils on a real transformer. The line (sometimes two or three are drawn) in the middle represent the magnetic link between the coils that is made by the soft iron core.

The Equation

There is a mathematical link between the number of turns and the voltages on each coil.

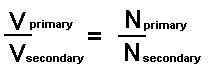
This ratio equation must be known for examination purposes. It doesn't matter which way up you write it, or which way round. Therefore always start with the unknown quantity in the top left position.

Example questions:

Example 1

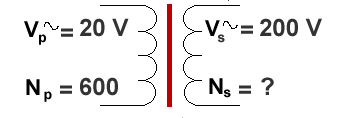
N_s is the unknown.

We therefore have to arrange the equation as follows:

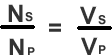
N_s / 600 = 200/20 = 10

So, N_s = 600 x 10 = 6000 (no unit as you are working out the number of turns)

In tests and examinations y ou must show your calculation in full in an examination to show that you understand how to use it.

There is a quick way to analyse this circuit and it is handy to do this as a quick check.

Look at the ratio relationship between the voltages and turns they will be the same for each.

Example 2

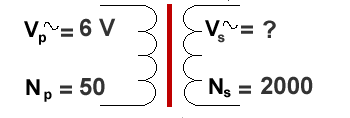
This time V_s is the unknown.

We therefore have to arrange the equation as follows:

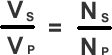
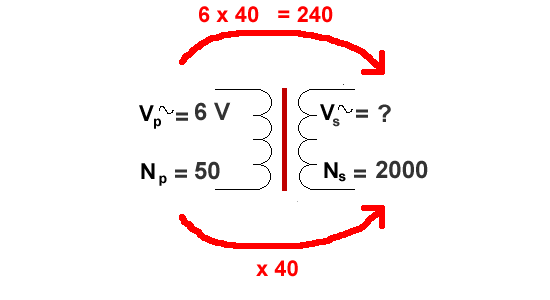
V_s / 6 = 2000/50 = 40

So, V_s = 6 x 40 = 240 volts (don't forget the unit!)

Lets try the check again

Example 3

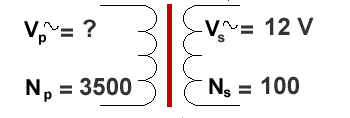
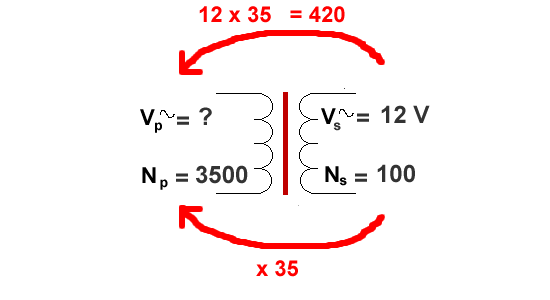
Now we have V_p as the unknown.

We therefore have to arrange the equation as follows:

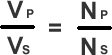
V_p / 12 = 3500/100 = 35

So, V_p = 12 x 35 = 420 volts (unit omission loses you marks!)

A quick check:

Example 4

Finally N_P as the unknown

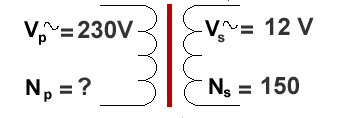
We must arrange the equation so N_P is at the top left

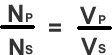
N_P / 150 = 230/12 = 19.17 (not a simple ratio here!)

So, N_p = 150 x 19.17 = 2876 (to the nearest turn… you can't have part turns!)

This is more difficult to do our 'quick-check' way

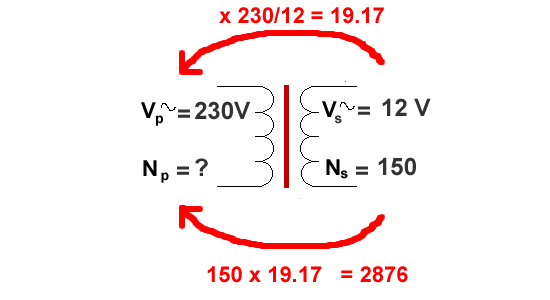
but still possible!